
Chapter 14 The parsimony method of tree estimation
This week we begin examining the tree-searching methods of tree estimation. Specifically, we will focus on the parsimony method.
14.1 Parsimony
Parsimony operates on the assumption that the tree containing the fewest sequence changes is the most accurate estimation of what really occurred. Essentially, parsimony assumes that characteristics shared by taxa are shared as the result of common ancestry. Sometimes this assumption is not valid, but often it is, particularly when there is not too much homoplasy (when two or more sequences or structures resemble each other but don’t have a common ancestral origin) or variation in rates between sites. Often there will be multiple equally parsimonious trees, in which case you can either make a consensus tree (a combination of all the equally parsimoniously trees), or pick one tree that is illustrative of the point being discussed. If you choose the second, make sure you mention the existence of the other, equally parsimonious trees!
Parsimony is technically not a phylogenetic method because it does not apply a substitution model to the sequence data. A proper parsimony tree does not scale the branches to the number of changes between taxa. Instead, all the taxa are lined up and the branches are however long they need to be in order for the taxa to line up.
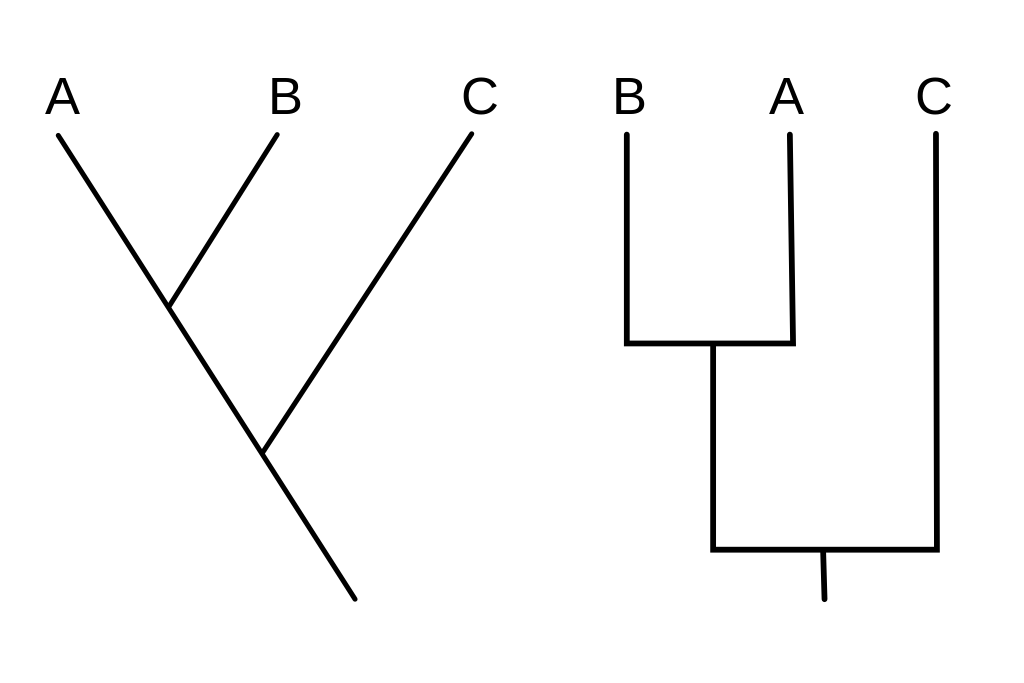
We will be scaling the branches in our parsimony trees to reflect the number of changes along each branch, so we will not be working with the parsimony method in its purest form.
The parsimony method is the backbone of the field known as “cladistics.” It’s largely fallen out of favor as phylogenetics is much more suited to analyzing genetic data. Parsimony still survives as a method of choice for researchers at the American Museum of Natural History and among paleontologists (or anyone who is inferring trees based on non-genetic data). The battle between cladistics proponents and phylogenetics proponents was so intense during the 1980s and 1990s my undergraduate advisor jokingly referred to it as the Clade Wars.
14.2 Tree searching methods
At the heart of the parsimony approach is the idea of tree searching. The parsimony algorithm starts with a random tree (sometimes even a neighbor joining tree, or a tree the researcher supplies). The starting tree is scored, then the tree topology is rearranged in some way to create a new tree. The new tree is scored; if its score is better than the previous tree, the new tree is kept. The process then continues until an optimum tree score is found or it reaches a set end point.
When a tree has only a small number of taxa, an exhaustive search of all possible topologies is possible. However, the number of possible topologies grows exponentially as the number of taxa increases (in his Phylogenetic Trees Made Easy manual, Barry G. Hall estimates that for a tree with just 10 taxa, there are more than 34 million possible rooted topologies). It rapidly becomes impractical to perform an exhaustive topology search to find the best tree. Instead, researchers have developed tree-searching algorithms to more quickly sort through all the possibilities.
14.2.1 Branch and bound
The branch and bound method, while not exhaustive, can still be time-consuming when dealing with more than ~10 taxa. In this approach, an initial random tree of all the taxa is created and scored.Then, the algorithm starts with a tree containing three taxa. Next, a branch containing a fourth taxon is inserted in all possible locations and each possible tree is scored. If none of the possible trees scores better than the initial random tree, this particular search is abandoned and a new starting tree of 3 taxa is created. If, however, any of these possible trees has a score smaller than the score of the initial random tree, the search continues and a fifth taxon is added. The process is repeated, with one change - if none of the trees with five taxa score low enough, then the search goes back to the four taxa tree and tries a different fifth taxon. This way, the initial work isn’t wasted.
14.2.2 Nearest Neighbor Interchange (NNI)
Nearest neighbor interchange algorithms take advantage of the fact that there are only three possible ways to connect four groups. A random starting tree is divided into four parts (or subtrees). These four subtrees are connected in all three possible ways. The most parsimonious arrangement is kept, and the new tree is then randomly subdivided into four new subtrees so the process can start again.
14.2.3 Subtree Pruning and Regrafting (SPR)
Subtree pruning and regrafting has two major steps. First, a random subtree is removed from the original starting tree; then, the subtree is inserted elsewhere on the main tree to create a new node. This rearranged tree is scored. If if is more parsimonious than the starting tree, the new tree is kept, and another subtree is pruned and regrafted.
14.2.4 Star decomposition
We actually saw the star decomposition method in the neighbor joining section. All taxa are connected together at a single node to form a star tree. Next, a pair of taxa are joined to form a new node and the tree is scored. This is repeated until all possible pairs have been evaluated. The best is kept and then another pair of taxa are joined, and the process continues.