
Chapter 12 The neighbor joining method of tree estimation
There are two basic types of tree estimation methods: distance methods (which includes neighbor joining, discussed here) and tree-searching methods (which we will cover in later sections). The first phylogenetic trees were built using distance methods. Strictly speaking, these methods can be considered phenetic methods, not phylogenetic methods, since these methods group taxa based on similarity instead of attempting to find the most likely tree. For all practical purposes, though, we can include neighbor joining in under the umbrella of phylogenetics.
In distance-based methods like neighbor joining, the genetic data is converted into a distance matrix, which is used to group taxa based on the genetic distance between them. Neighbor joining specifically works via star decomposition. Let’s take a look at an example (adapted from (Fred Opperdoes)[http://www.deduveinstitute.be/~opperd/private/neighbor.html]).
We have 5 taxa (A,B,C,D, and E) for which we would like to infer a phylogeny. We’ve calculated the following distances among all the taxa:

The shortest distance between any taxa is 13, which means that A and B are most closely related to each other and will form our first group. We begin with all the taxa forming a star shape, and then we add a branch that connects A and B.
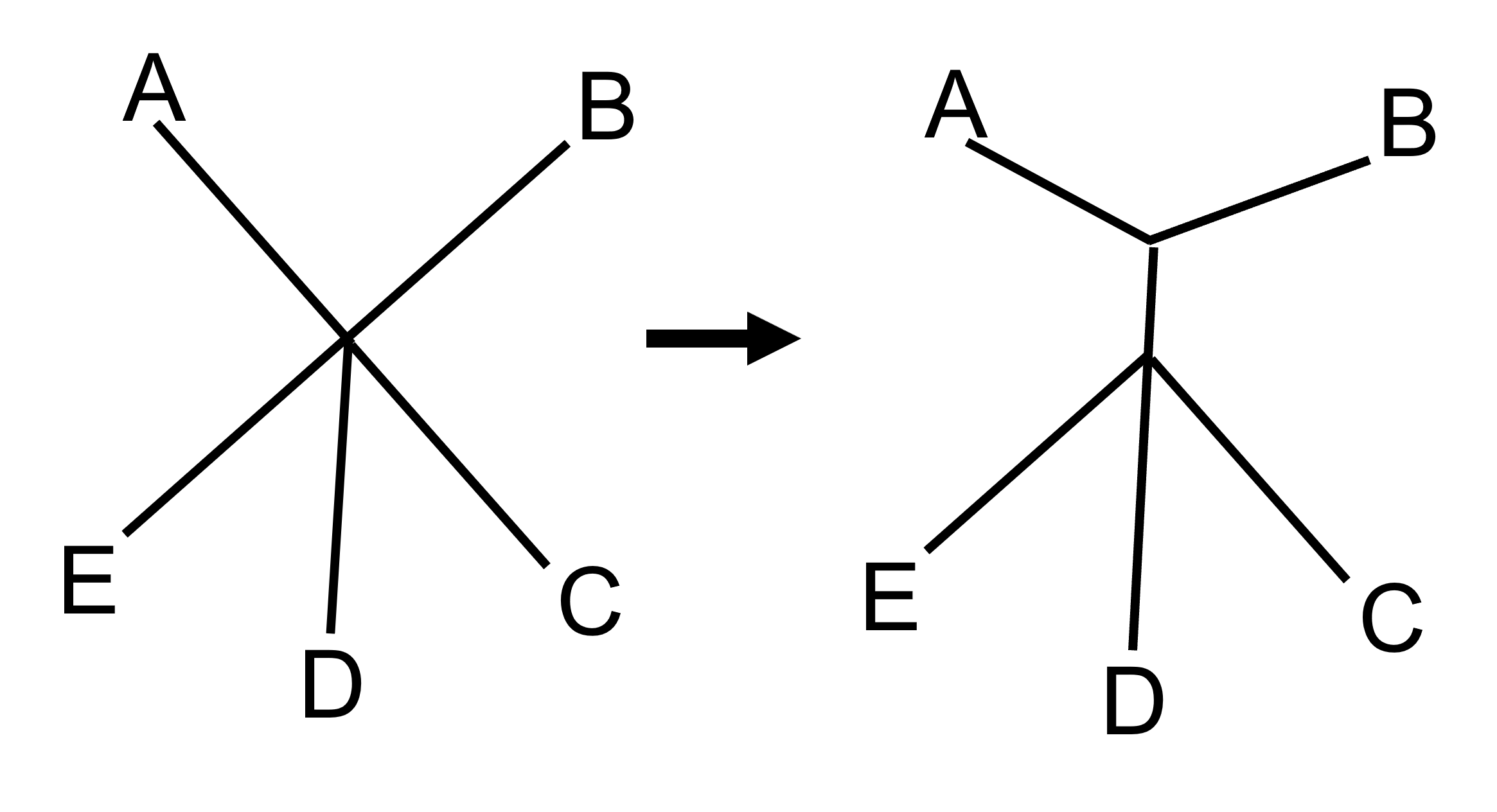
We keep grouping taxa until the entire star has been resolved into bifurcating branches (nodes that connect two, and only two, branches). For our example tree, we eventually end up with this tree:
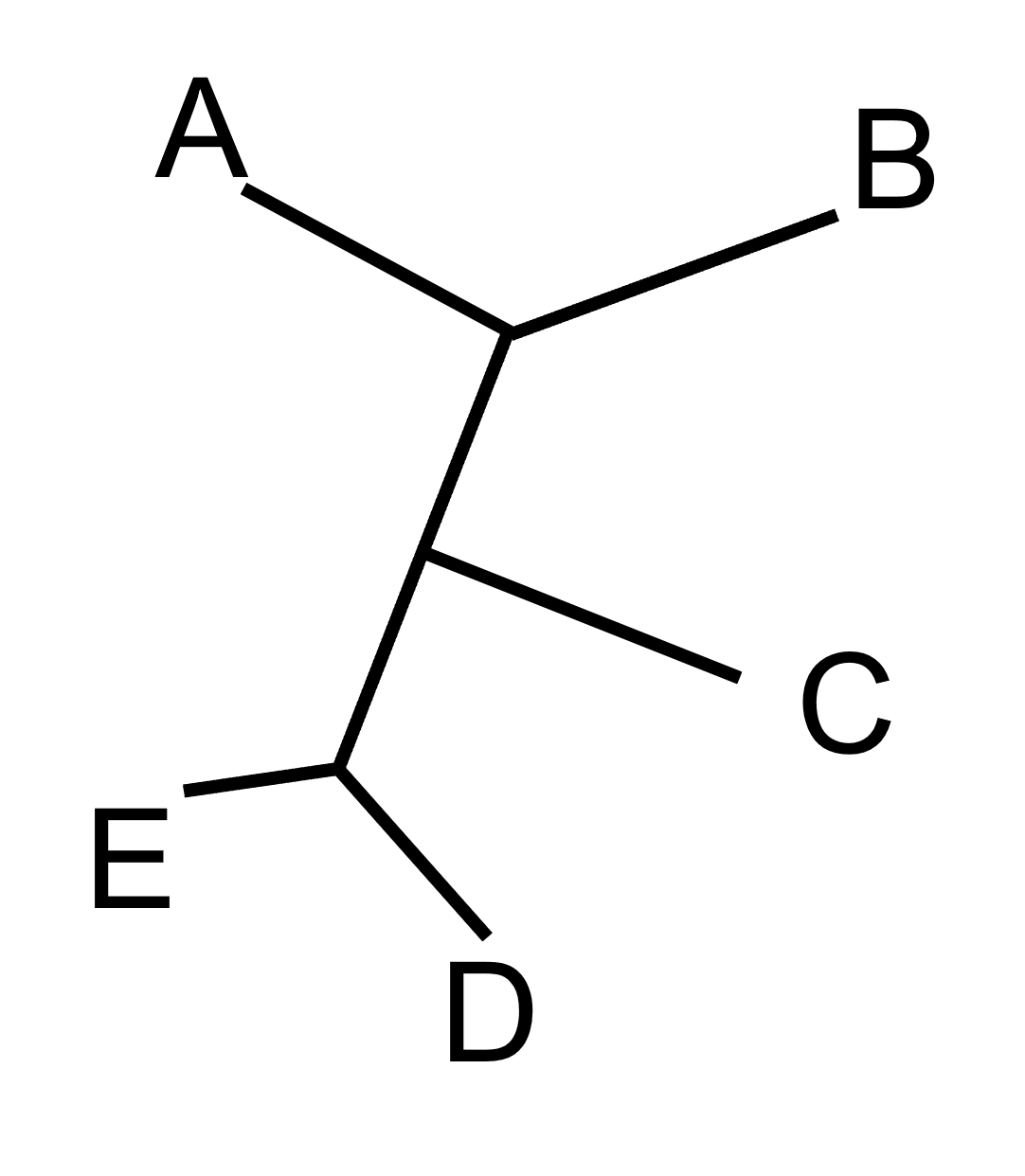
The neighbor joining method is very fast, requires very few computational resources, and is statistically consistent. It will also always result in only a single tree topology. Unfortunately, many people will become overly confident that the single neighbor joining tree is the true tree, which is not necessarily true. Nowadays, most researchers might start their analysis with a neighbor joining tree, but they generally go on to infer trees using one of the other methods.
There is another type of distance method you might hear about called UPGMA (unweighted pair group method with arithmetic mean). This is a hierarchical clustering method. However, the tree built using UPGMA depends greatly on the order in which the taxa are added, unlike the neighbor joining method (which will result in the same tree no matter what order the samples are added). As a result, the UPGMA method is almost never used in phylogenetics today.
12.1 Models of molecular evolution
In the example above, we kind of glossed over the process of converting DNA sequence into genetic distances. In its simplest form, every mutation is given a value, and the total value of all mutations is then used to calculate a genetic distance.
But wait, you might be thinking. How do researchers decide what value to assign each mutation? Are all mutations given the same value, or do some changes “cost” more than others? Aren’t some mutations considered more unlikely than others? These are all excellent questions that should be considered whenever dealing with phylogenetic analysis. Luckily, we don’t have to answer all these questions ourselves. Instead, we can look at published models of molecular evolution (also called substitution models) and decide which model fits our data the best.
12.1.1 JC69
A model of molecular evolution is a set of rules that determines how much each mutation costs relative to all other mutations. One of the earliest published models is the JC69 model (sometimes written as JC), proposed by Jukes and Cantor in 1969. The JC69 model assumes equal base frequencies (that is, each nucleotide makes up 25% of the bases in the DNA sequence), as well as equal mutation rates. A mutation of an A to a T is the same as the mutation as a T to an A or an A to a C. As a result, the JC69 model has only 1 parameter - the mutation rate.
12.1.2 K2P
Many other models of molecular evolution have been published since JC69. One of the more popular ones is the Kimura two-parameter model (also called K80, or K2P). This model still assumes equal base frequencies, but allows for a distinct mutation rate for transitions (mutations between purines or pyrimidines) and a different mutation rate for tranversions (mutations from purine to pyrimidine, or vice versa). As you might have guessed from the name, this particular model has two parameters.
12.1.3 GTR
One of the most complex models you might come across is the general time reversible model, or GTR. This model is extremely flexible but also parameter-heavy. There are no assumptions about base frequencies, and each possible mutation is given its own mutation rate. (A quick note: the mutation rate from A to G is the same as the mutation rate from G to A in this model.) As a result, this model has 9 parameters: 6 mutation rates + 3 base frequencies. (Because the sum of the 4 base frequencies must equal 1, we only have to describe 3 of them in order to calculate all 4. That’s why we only need 3 parameters to model the base frequencies for GTR.)
12.1.4 Other parameters
Sometimes you will run across a model that has “+ I” added to it (like GTR + I). The “I” refers to a invariant sites parameter. In these models, each base has a certain probability of being invariate, or unlikely to mutate.
Another option you might see is using a gamma distribution to estimate how many times any given base in a sequence might mutate. We often think of mutation as a one-and-done process, where a nucleotide might mutate only once. This isn’t a bad assumption; in fact, given that mutation is so rare, it is extremely unlikely for a nucleotide to mutate multiple times, though it does happen (particularly as divergence times between taxa increase). A solution to this dilemma is to include a parameter that describes how many times a particular nucleotide has undergone mutation. A gamma distribution is used because the highest probability is found in the smallest values of x, with a low probability of larger values of x (which would be multiple mutation hits at the same nucleotide). A model using a gamma distribution with have a “+ G”.
Finally, some models with have a “+ SS” added to it. The SS indicates a site-specific variation parameter. These models will estimate different mutation rates for each codon position. Site-specific models are much less common than models that include invariate sites parameters or a $ parameter.
12.1.5 How do I choose a model?
There are enough substitution models out there that it can be a bit overwhelming to pick one for your phylogenetic analyses. (The models discussed above are in no way an exhaustive list.) Many researchers will have a favorite model they use, while others will rely model test programs to tell them which model of molecular evolution best fits their data. Although GTR + I + $ might be the most biologically realistic model, it is also parameter-heavy and may not be the best choice when dealing with a sequence alignment that includes only a small number of phylogenetically-informative sites.
## Determining distance matrix based on shared 10-mers:
## ================================================================================
##
## Time difference of 0.01 secs
##
## Clustering into groups by similarity:
## ================================================================================
##
## Time difference of 0 secs
##
## Aligning Sequences:
## ================================================================================
##
## Time difference of 0.32 secs
##
## Iteration 1 of 2:
##
## Determining distance matrix based on alignment:
## ================================================================================
##
## Time difference of 0 secs
##
## Reclustering into groups by similarity:
## ================================================================================
##
## Time difference of 0 secs
##
## Realigning Sequences:
## ================================================================================
##
## Time difference of 0.56 secs
##
## Iteration 2 of 2:
##
## Determining distance matrix based on alignment:
## ================================================================================
##
## Time difference of 0 secs
##
## Reclustering into groups by similarity:
## ================================================================================
##
## Time difference of 0 secs
##
## Realigning Sequences:
## ================================================================================
##
## Time difference of 0.76 secs
##
## Refining the alignment:
## ================================================================================
##
## Time difference of 0.82 secs